01 회귀 소개
통계학: 여러개의 독립변수와 한개의 종속 변수 간의 상관관계를 리모델링하는 기법을 통칭
Y=W1*X1+W2*X2.....+Wn*Xn 일 경우 Y는 종속변수, 아파트 가격, X1, X2는 독립변수를 의미하며 W1, W1..Wn은 독립변수의 값에 영향을 미치는 회귀 계수(Regression coefficients)를 나타냅니다. 머신러닝 회귀 예측의 핵심은 주어진 피처와 결정값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것

지도학습은 크게 classification - 예측값이 카테고리와 같은 이산형 클래스와 regression- 예측값이 연속형 숫자값으로 나뉘어짐.
선형회귀는 실제값과 예측값의 차이를 최소화하는 직선형 회귀선을 최적화하는 방식, Regularization 방법에 따라 별ㄷ의 유형으로 나뉘며, 규제는 일반적인 선형회귀의 과적합을 해결하기 위해 회귀 계수에 페널티 값을 적용하는 것.
02 단순 선형 회귀를 통한 회귀 이해
단순 선형의 경우 독립변수도 하나, 종속 변수도 하나이기에 선형(직선형태의 관계로 표현)

2차원 평면세어 특정 기울기와 1차 절편을 가진 1차 함수식으로 모델링 가능, 독립변수가 1개인 단순 선형회귀에선 그림의 수식으로 표현. 실제 값과 회귀 모델의 차이에 따른 오류값을 남은 오류, 잔차라고 부름. 최적의 회귀 모델: 전체 데이터의 잔차 합이 최소가 되는 모델을 만듦 -> 오류 값이 최소가 될 수 있는 최적의 회귀 계수 생성

오류합을 구하기 위해서는 오류가 +,-가 되기때문에 단순히 더했다가 오류합이 줄어들수 있어서 절댓값을 취하는(Mean Absolute Error), 오류값의 제곱을 도해서 더하는 방식(RSS)을 취합니다. Residual Sum of Square(RSS)은 ERror^2와 같습니다.

RSS을 최소로 하는 것, w0 w1 즉 회귀계수를 학습을 통해서 찾는것이 머신러닝 기반 회기의 핵심사항
RSS(Cost)비용이며, w변수(회귀 계수)로 구성되는 RSS을 비용함수라고 해, 머신 러닝 회귀는 데이터를 계속 학습하며 이 비용 함수가 반환하는 값을 지속해서 감소시키고 더 이상 감소하지 않은 최소의 오류값을 구해서 손실함수(Loss Function)이라고 함.
03 비용 최소화 하기- 경사 하강법(Gradient Descent)
비용 함수가 최소화되는 w 파라미터를 구하기 위해선, 경사하강법 사용: 고차원 방정식에 대한 문제를 해결해주며 비용함수 RSS을 최소화, '데이터를 기반으로 알고리즘이 스스로 학습','점진적인 하강'으로 반복적인 계산을 통해 파라미터 값을 업데이트하며 오류값이 최소가 되는 파라미터를 구함.
경사하강법: 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 w파라미터를 지속해서 보정해나감.
"어떻게 하면 오류가 작아지는 방향으로 W 값을 보정할 수 있을까?"가 경사하강법의 핵심

비용함수를 미분해서 미분 함수의 최소값을 구하는것: 편미분 사용
다음 그림은 비용함수 RSS을 w1, w0으로 편미분한 결과이다.
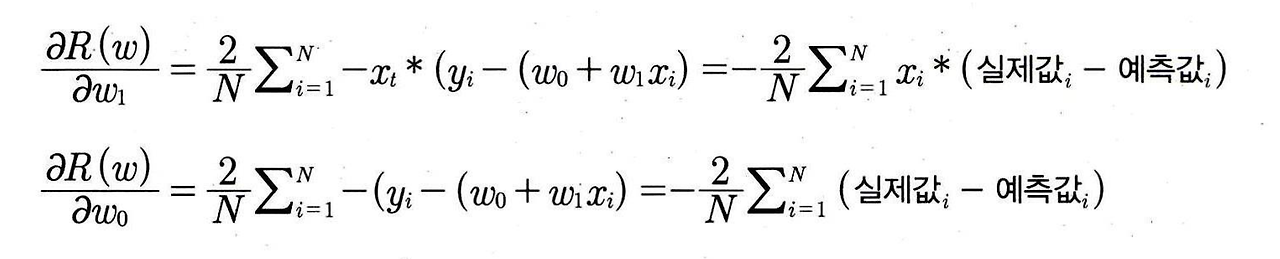
편미분 값을 업데이트 하면서 비용함수가 최소가 되는 w1,w0을 구한다 업데이트는 새로운 w1을 이전 w1에서 편미분 결과값을 마이너스하면서 적용한다. 편미분 값이 너무 클수있기 때문에 '학습률'이라는 보정 계수를 구해서 반복적으로 족용하며 비용함수가 최소가 되는 값을 찾는다.
코드
#03 경사하강법 Gradient Descent
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
# y = 4x+6을 근사 (w=1, w0=6). 임의 값은 노이즈를 위해 만듦
X=2*np.random.rand(100,1)
y=6+4*X+np.random.randn(100,1)
#X,y데이터 세트 산점도로 시각화
plt.scatter(X,y)def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred)) / N
return cost#w1과 w0을 업데이트할 w1_update, w0_update를 반환.
def get_weight_updates(w1,w0,X,y,learning_rate=0.01):
N = len(y)
#먼저 w1_update, w_update를 각각 w1, w0의 shape와 동일한 크기를 가진 0값으로 초기화
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
#예측 배열하고 계산하고 예측과 실제 값의 차이 계산
y_pred=np.dot(X,w1.T)+w0
diff=y-y_pred
#w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진걸 생성
w0_factors = np.ones((N,1))
#w1 w0를 업데이트할 w1_update와 w0_update를 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
W0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w0_update# 입력 인자 iters로 주어진 횟수만큼 반복적으로 w1과 w0를 업데이트 적용함.
def gradient_descent_steps(X, y, iters=10000):
# w0와 w1을 모두 0으로 초기화.
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
# 인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출하여 w1, w0 업데이트 수행.
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1:{0:.3f} w0:{1:.3f}".format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))plt.scatter(X,y)
plt.plot(X,y_pred)
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
prev_cost = 100000
iter_index =0
for ind in range(iters):
np.random.seed(ind)
# 전체 X, y 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_X, sample_y로 저장
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
# 랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000)
print("w1:",round(w1[0,0],3),"w0:",round(w0[0,0],3))
y_pred = w1[0,0] * X + w0
print('Stochastic Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
04 사이킷런 LinearRegression을 이용한 보스턴 주택 가격 예측
Linear Regressino 클래스는 예측값과 실제 값의 RSS을 최소화해 OLS(Ordinary Least Squares)방식으로 구현한 클래스이며, fit메서드로 X,y배열을 입력받으면 회귀 계수 W를 coef_속성에 저장합니다.
Ordinary Least Squares 기반의 회귀 계수 계산은 입력 피처의 독립성에 많은 영향을 받고 상관관계가 매우 높은 경우 분산이 커져서 오류에 매우 민감해지며, 이런 현상을 다중 공선성(multi-collinearity)문제라고 한다. 상관관계가 높은 피처의 경우 독립적인 중요한 피처만 남기고 제거하거나 규제를 적용한다.
회귀 평가 지표
회귀 평가 지표는 실제 값과 회귀 예측값의 차이를 기반으로 한 지표가 중심이됨. 실제 값과 예측값의 차이를 그냥 더할 경우 상쇄될수 있기 때문에 절댓갑 평균이나 제곱, 또는 제곱한 후 루트를 씌운 평균값을 구하기도 함.

RMSE의 경우 MSE에 지곱근을 씌워서 계산하는 함수 직접 만들어야함.
Linear Regression을 이용해 보스턴 주택 가격 회귀 구현
import numpy as np
import matplotlib.pyplot as plt # plt를 제대로 임포트합니다.
import pandas as pd
import seaborn as sns
from scipy import stats
%matplotlib inline
# boston.csv 파일 로드
bostonDF = pd.read_csv('boston.csv')
# bostonDF 데이터 확인
print('Boston 데이터셋 크기 :', bostonDF.shape)
bostonDF.head()# 2개의 행과 4개의 열을 가진 subplots를 이용. axs는 4x2개의 ax를 가짐.
fig, axs = plt.subplots(figsize=(16,8) , ncols=4 , nrows=2)
lm_features = ['RM','ZN','INDUS','NOX','AGE','PTRATIO','LSTAT','RAD']
for i , feature in enumerate(lm_features):
row = int(i/4)
col = i%4
# 시본의 regplot을 이용해 산점도와 선형 회귀 직선을 함께 표현
sns.regplot(x=feature , y='MEDV',data=bostonDF , ax=axs[row][col])from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error , r2_score
y_target = bostonDF['MEDV']
X_data = bostonDF.drop(['MEDV'],axis=1,inplace=False)
X_train , X_test , y_train , y_test = train_test_split(X_data , y_target ,test_size=0.3, random_state=156)
# Linear Regression OLS로 학습/예측/평가 수행.
lr = LinearRegression()
lr.fit(X_train ,y_train )
y_preds = lr.predict(X_test)
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)
print('MSE : {0:.3f} , RMSE : {1:.3F}'.format(mse , rmse))
print('Variance score : {0:.3f}'.format(r2_score(y_test, y_preds)))print('절편 값:',lr.intercept_)
print('회귀 계수값:', np.round(lr.coef_, 1))# 회귀 계수를 큰 값 순으로 정렬하기 위해 Series로 생성. index가 컬럼명에 유의
coeff = pd.Series(data=np.round(lr.coef_, 1), index=X_data.columns )
coeff.sort_values(ascending=False)from sklearn.model_selection import cross_val_score
y_target = bostonDF['MEDV']
X_data = bostonDF.drop(['MEDV'],axis=1,inplace=False)
lr = LinearRegression()
# cross_val_score( )로 5 Fold 셋으로 MSE 를 구한 뒤 이를 기반으로 다시 RMSE 구함.
neg_mse_scores = cross_val_score(lr, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
# cross_val_score(scoring="neg_mean_squared_error")로 반환된 값은 모두 음수
print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 2))
print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores, 2))
print(' 5 folds 의 평균 RMSE : {0:.3f} '.format(avg_rmse))
05 다항 회귀와 과(대)적합/과소적합이해
독립변수의 단항식이 아닌 2차, 3차와 같은 다항식으로 표현하는것을 다항 회귀, 회귀 계수가 선형인지 비선형인지를 보았을때, 다항회귀는 선형 회귀
polynomialFeatures 클래스를 통해 피처를 다항식피처로 변환해서 degree 파라미터를 통해 입력 받은 단항식 피처를 degree에 해당하는 다항식 피처로 변환.
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
X= np.arange(4).reshape(2,2)
print('일차 단항식 계수 피처:\n',X)
poly=PolynomialFeatures(degree=2)
poly.fit(X)
poly_ftr = poly.transform(X)
print('변환된 2차 다항식 계수 피처:\n', poly_ftr)def polynomial_func(X):
y=1+2*X[:,0]+3*X[:,0]**2+4*X[:,1]**3
return y
X=np.arange(4).reshape(2,2)
print('일차 단항식 계수 피처:\n',X)
y=polynomial_func(X)
print('삼차 다항식 결정값: \n',y)#3차 다항식 변환
poly_ftr=PolynomialFeatures(degree=3).fit_transform(X)
print('3차 다항식 계수 feature: \n',poly_ftr)
#linear regression에 3차 다항식 계수 feature와 3차 다항식 결정값으로 학습 후 회귀 계수 확인
model = LinearRegression()
model.fit(poly_ftr,y)
print('Poynomial 회귀 계수]n', np.round(model.coef_,2))
print('Polynomial 회귀 Shape : ', model.coef_.shape)from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np
def polynomial_func(X):
y=1+2*X[:,0]+3*X[:,0]**2+4*X[:,1]**3
return y
#Pipieline 객체로 Streamline하게 Polynomial Feature 변환과 linear regression을 연결
model = Pipeline([('poly',PolynomialFeatures(degree=3)),
('linear',LinearRegression())])
X=np.arange(4).reshape(2,2)
y=polynomial_func(X)
model = model.fit(X,y)
print('Polynomial 회귀 계수\n', np.round(model.named_steps['linear'].coef_,2))
다항 회귀는 피처의 직선적 관계가 아닌 복잡한 다항 관계를 모델링 할 수 있음. 다항식의 차수가 높아질수록 복잡한 피처간의 관계까지 모델링이 가능하나, 차수를 높일수록 학습 데이터에만 너무 맞춘학습이 이뤄져서 과적합이 발생할 수 있음.
#데이터 세트와 다항 회귀의 차수를 변화시키면서 회귀 예측 곡선과 예측 정확도를 비교하는 예제 코드는 추후 첨부. p.315
import numpy as np
import maplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Regression
from sklearn.model_selection import cross_val_score
%matplotlib inline
#임의의 값으로 구성된 X값에 대해 코사인 변환값을 반환.
def true_fun(X):
return np.com(1.5*np.pi*X)
#X는 0부터 1까지 30개의 임의의 값을 순서대로 샘플링한 데이터
np.random.seed(0)
n_samples=30
X=np.sort(np.random.rand(n_samples))
#y값은 코사인 기반의 true_fun()에서 약간의 노이즈 변동 값을 더한 값
y=true_fun(X)+np.random.randn(n_samples)*0.1plt.scatter(X, y)plt.figure(figsize=(14, 5))
degrees = [1, 4, 15]
# 다항 회귀의 차수(degree)를 1, 4, 15로 각각 변화시키면서 비교합니다.
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i + 1)
plt.setp(ax, xticks=(), yticks=())
# 개별 degree별로 Polynomial 변환합니다.
polynomial_features = PolynomialFeatures(degree=degrees[i], include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)])
pipeline.fit(X.reshape(-1, 1), y)
# 교차 검증으로 다항 회귀를 평가합니다.
scores = cross_val_score(pipeline, X.reshape(-1,1), y,scoring="neg_mean_squared_error", cv=10)
coefficients = pipeline.named_steps['linear_regression'].coef_
print('\nDegree {0} 회귀 계수는 {1} 입니다.'.format(degrees[i], np.round(coefficients),2))
print('Degree {0} MSE 는 {1:.2f} 입니다.'.format(degrees[i] , -1*np.mean(scores)))
# 0 부터 1까지 테스트 데이터 세트를 100개로 나눠 예측을 수행합니다.
# 테스트 데이터 세트에 회귀 예측을 수행하고 예측 곡선과 실제 곡선을 그려서 비교합니다.
X_test = np.linspace(0, 1, 100)
# 예측값 곡선
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
# 실제 값 곡선
plt.plot(X_test, true_fun(X_test), '--', label="True function")
plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
plt.xlabel("x"); plt.ylabel("y"); plt.xlim((0, 1)); plt.ylim((-2, 2)); plt.legend(loc="best")
plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(degrees[i], -scores.mean(), scores.std()))
plt.show()편향-분산 트레이드오프(Bias-Variance Trade off)
고편향(High Bias): 단순화된 모델로서 지나치게 한 방향으로 치우친 경향
고분산(High Variance): 학습 데이터 하나하나의 특성을 반양해 매우 복잡하지만, 높은 변동성을 가지게 됨.

편향이 높을 경우 분산이 낮아져서 과소적합 <-> 분산이 높으면 편향이 낮아져서 과적합
전체 오류값(Total Error)의 변화: 편향이 너무 높으면 전체 오류가 높고, 편향을 점점 낮추면 분산이 높아지고, 전체 오류도 낮아지게됨. 편향을 낮추고 분산을 높이면서 전체 오류가 낮아지는 '골디락스'지점을 통과하며 분산을 지속적으로 높이면 전체 오류값이 증가하면서 예측 성능이 다시 저하됨.
06 규제 선형모델 - 릿지, 라쏘, 엘라스틱넷
규제 선형 모델: RSS를 최소화하는것만 고려하다보니, 학습 데이터에 맞추게 되고, 회귀 계수가 커져서 테스트 데이터세트에서 예측 성능이 저하됨. 반영하기 위해, 비용함수는 학습데이터의 잔차 오류값을 최소로하는 RSS 초소화 방법과 과적화를 방지하기 위한 균형이 필요함

비용 함수 목표 =
alpha: 학습 데이터 적합정도와 회귀 계수 값의 크기 제어를 수행하는 튜닝 파라미터. 0일경우, W가 커져도 alpha가 0이 되어 비용함수는 min(RSS(W)), 무한대일 경우 alppa도 무한대가 되므로 비용함수는 W를 0에 가깝게 최소화해야함.
따라서, 알파를 0에서부터 지속적으로 값을 증가시키면 회귀 계수 값의 크기를 감소시키고, 페널티를 부여해 과적합을 개선함 = (Regularization)

Regularized Linear Model - Ridge Regression
# 앞의 LinearRegression예제에서 분할한 feature 데이터 셋인 X_data과 Target 데이터 셋인 Y_target 데이터셋을 그대로 이용
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
# boston 데이타셋 로드
boston = load_boston()
# boston 데이타셋 DataFrame 변환
bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names)
# boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가함.
bostonDF['PRICE'] = boston.target
print('Boston 데이타셋 크기 :',bostonDF.shape)
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)
ridge = Ridge(alpha = 10)
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 3))
print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores,3))
print(' 5 folds 의 평균 RMSE : {0:.3f} '.format(avg_rmse))# Ridge에 사용될 alpha 파라미터의 값들을 정의
alphas = [0 , 0.1 , 1 , 10 , 100]
# alphas list 값을 iteration하면서 alpha에 따른 평균 rmse 구함.
for alpha in alphas :
ridge = Ridge(alpha = alpha)
#cross_val_score를 이용하여 5 fold의 평균 RMSE 계산
neg_mse_scores = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
print('alpha {0} 일 때 5 folds 의 평균 RMSE : {1:.3f} '.format(alpha,avg_rmse))# 각 alpha에 따른 회귀 계수 값을 시각화하기 위해 5개의 열로 된 맷플롯립 축 생성
fig , axs = plt.subplots(figsize=(18,6) , nrows=1 , ncols=5)
# 각 alpha에 따른 회귀 계수 값을 데이터로 저장하기 위한 DataFrame 생성
coeff_df = pd.DataFrame()
# alphas 리스트 값을 차례로 입력해 회귀 계수 값 시각화 및 데이터 저장. pos는 axis의 위치 지정
for pos , alpha in enumerate(alphas) :
ridge = Ridge(alpha = alpha)
ridge.fit(X_data , y_target)
# alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가.
coeff = pd.Series(data=ridge.coef_ , index=X_data.columns )
colname='alpha:'+str(alpha)
coeff_df[colname] = coeff
# 막대 그래프로 각 alpha 값에서의 회귀 계수를 시각화. 회귀 계수값이 높은 순으로 표현
coeff = coeff.sort_values(ascending=False)
axs[pos].set_title(colname)
axs[pos].set_xlim(-3,6)
sns.barplot(x=coeff.values , y=coeff.index, ax=axs[pos])
# for 문 바깥에서 맷플롯립의 show 호출 및 alpha에 따른 피처별 회귀 계수를 DataFrame으로 표시
plt.show()ridge_alphas = [0 , 0.1 , 1 , 10 , 100]
sort_column = 'alpha:'+str(ridge_alphas[0])
coeff_df.sort_values(by=sort_column, ascending=False)
Regularized Linear Model - Lasso Regression
from sklearn.linear_model import Lasso, ElasticNet
# alpha값에 따른 회귀 모델의 폴드 평균 RMSE를 출력하고 회귀 계수값들을 DataFrame으로 반환
def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None,
verbose=True, return_coeff=True):
coeff_df = pd.DataFrame()
if verbose : print('####### ', model_name , '#######')
for param in params:
if model_name =='Ridge': model = Ridge(alpha=param)
elif model_name =='Lasso': model = Lasso(alpha=param)
elif model_name =='ElasticNet': model = ElasticNet(alpha=param, l1_ratio=0.7)
neg_mse_scores = cross_val_score(model, X_data_n,
y_target_n, scoring="neg_mean_squared_error", cv = 5)
avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores))
print('alpha {0}일 때 5 폴드 세트의 평균 RMSE: {1:.3f} '.format(param, avg_rmse))
# cross_val_score는 evaluation metric만 반환하므로 모델을 다시 학습하여 회귀 계수 추출
model.fit(X_data_n , y_target_n)
if return_coeff:
# alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가.
coeff = pd.Series(data=model.coef_ , index=X_data_n.columns )
colname='alpha:'+str(param)
coeff_df[colname] = coeff
return coeff_df
# end of get_linear_regre_eval# 라쏘에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출
lasso_alphas = [ 0.07, 0.1, 0.5, 1, 3]
coeff_lasso_df =get_linear_reg_eval('Lasso', params=lasso_alphas, X_data_n=X_data, y_target_n=y_target)print(lasso_alphas)# 반환된 coeff_lasso_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력
sort_column = 'alpha:'+str(lasso_alphas[0])
coeff_lasso_df.sort_values(by=sort_column, ascending=False)
Regularized Linear Model -Elastic Net Regression
엘라스틱넷 회귀는 L2+L1 규제 결합, 최소화하는 W를 찾는것이므로, 서로 라쏘 회귀의 상관관계가 높은 피처들의 경우 중요 피처만을 셀렉션하고, 다른 피처들은 모두 회귀 계수를 0으로 만드는 성향이 강함. 따라서 회귀 계수의 값이 급격히 변동할 수 있음을 완화하기 위해 L2를 추가.
단점: 수행시간이 상대적으로 오래 걸림.

# 엘라스틱넷에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출
# l1_ratio는 0.7로 고정
elastic_alphas = [ 0.07, 0.1, 0.5, 1, 3]
coeff_elastic_df =get_linear_reg_eval('ElasticNet', params=elastic_alphas,
X_data_n=X_data, y_target_n=y_target)# 반환된 coeff_elastic_df를 첫번째 컬럼순으로 내림차순 정렬하여 회귀계수 DataFrame출력
sort_column = 'alpha:'+str(elastic_alphas[0])
coeff_elastic_df.sort_values(by=sort_column, ascending=False)
07 로지스틱 회귀
로지스틱 회귀: 선형 회귀 방식을 분류에 적용한 알고리즘, 분류에 사용되며 선형회귀 계열, S자 형태를 갖고 있음. 시그모이드 함수의 X 값이 아무리 커지거나 작아져도 y값은 항상 0과 1사이만의 값을 반환.
선형 회귀의 학습을 통해 최적선을 찾는것이 아니라, 시그모이드(Sigmoid) 함수 최적선을 찾고 함수의 반환값을 확률로 간주해 확률에 따라 분류를 결정.

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
cancer = load_breast_cancer()from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# StandardScaler( )로 평균이 0, 분산 1로 데이터 분포도 변환
scaler = StandardScaler()
data_scaled = scaler.fit_transform(cancer.data)
X_train , X_test, y_train , y_test = train_test_split(data_scaled, cancer.target, test_size=0.3, random_state=0)from sklearn.metrics import accuracy_score, roc_auc_score
# 로지스틱 회귀를 이용하여 학습 및 예측 수행.
lr_clf = LogisticRegression()
lr_clf.fit(X_train, y_train)
lr_preds = lr_clf.predict(X_test)
# accuracy와 roc_auc 측정
print('accuracy: {:0.3f}'.format(accuracy_score(y_test, lr_preds)))
print('roc_auc: {:0.3f}'.format(roc_auc_score(y_test , lr_preds)))from sklearn.model_selection import GridSearchCV
params={'penalty':['l2', 'l1'],
'C':[0.01, 0.1, 1, 1, 5, 10]}
grid_clf = GridSearchCV(lr_clf, param_grid=params, scoring='accuracy', cv=3 )
grid_clf.fit(data_scaled, cancer.target)
print('최적 하이퍼 파라미터:{0}, 최적 평균 정확도:{1:.3f}'.format(grid_clf.best_params_,
grid_clf.best_score_))08 회귀 트리
머신러닝 기반의 회귀 = 회귀 계수를 기반으로 하는 최적 회귀 함수를 도출하는것이 목표
회귀 함수를 기반으로 하지 않고, 결정 트리와 같이 트리를 기반으로 하는 회귀 방식: 회귀 트리 이용
회귀를 위한 트리 생성하고, 기반으로 예측, 분류트리와 비슷하나 리프노드에서 예측 결정값을 만들때, 회귀 트리는 리프 노드에 속한 데이터값의 평균값을 구해 회귀 예측값을 계산.

리프 노드 생성 기준에 부합하는 트리 분할이 완료되었다면 리프 노드에 소속된 데이터 값의 평균값을 구해 최종적으로 리프 노드의 결정값으로 할당. 결정트리, 랜덤 포레스트, GBM, XGBoost, LightGBM 모두 분류 뿐만 아니라 회귀도 가능. Estimator 클래스를 사용해서 회귀와 분류 가능.
from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestRegressor
import pandas as pd
import numpy as np
# 보스턴 데이터 세트 로드
boston = load_boston()
bostonDF = pd.DataFrame(boston.data, columns = boston.feature_names)
bostonDF['PRICE'] = boston.target
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'], axis=1,inplace=False)
rf = RandomForestRegressor(random_state=0, n_estimators=1000)
neg_mse_scores = cross_val_score(rf, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print(' 5 교차 검증의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 2))
print(' 5 교차 검증의 개별 RMSE scores : ', np.round(rmse_scores, 2))
print(' 5 교차 검증의 평균 RMSE : {0:.3f} '.format(avg_rmse))def get_model_cv_prediction(model, X_data, y_target):
neg_mse_scores = cross_val_score(model, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
print('##### ',model.__class__.__name__ , ' #####')
print(' 5 교차 검증의 평균 RMSE : {0:.3f} '.format(avg_rmse))from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import GradientBoostingRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
dt_reg = DecisionTreeRegressor(random_state=0, max_depth=4)
rf_reg = RandomForestRegressor(random_state=0, n_estimators=1000)
gb_reg = GradientBoostingRegressor(random_state=0, n_estimators=1000)
xgb_reg = XGBRegressor(n_estimators=1000)
lgb_reg = LGBMRegressor(n_estimators=1000)
# 트리 기반의 회귀 모델을 반복하면서 평가 수행
models = [dt_reg, rf_reg, gb_reg, xgb_reg, lgb_reg]
for model in models:
get_model_cv_prediction(model, X_data, y_target)09 회귀 실습 자전거 대여 수요 예측
케글의 자전거 대여수요 예측을 통해 선형 회귀와 트리 기반 회귀 비교
데이터 클렌징 및 가공
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
bike_df = pd.read_csv('./bike_train.csv')
print(bike_df.shape)
bike_df.head(3)bike_df.info()# 문자열을 datetime 타입으로 변경.
bike_df['datetime'] = bike_df.datetime.apply(pd.to_datetime)
# datetime 타입에서 년, 월, 일, 시간 추출
bike_df['year'] = bike_df.datetime.apply(lambda x : x.year)
bike_df['month'] = bike_df.datetime.apply(lambda x : x.month)
bike_df['day'] = bike_df.datetime.apply(lambda x : x.day)
bike_df['hour'] = bike_df.datetime.apply(lambda x: x.hour)
bike_df.head(3)drop_columns = ['datetime','casual','registered']
bike_df.drop(drop_columns, axis=1,inplace=True)from sklearn.metrics import mean_squared_error, mean_absolute_error
# log 값 변환 시 NaN등의 이슈로 log() 가 아닌 log1p() 를 이용하여 RMSLE 계산
def rmsle(y, pred):
log_y = np.log1p(y)
log_pred = np.log1p(pred)
squared_error = (log_y - log_pred) ** 2
rmsle = np.sqrt(np.mean(squared_error))
return rmsle
# 사이킷런의 mean_square_error() 를 이용하여 RMSE 계산
def rmse(y,pred):
return np.sqrt(mean_squared_error(y,pred))
# MSE, RMSE, RMSLE 를 모두 계산
def evaluate_regr(y,pred):
rmsle_val = rmsle(y,pred)
rmse_val = rmse(y,pred)
# MAE 는 scikit learn의 mean_absolute_error() 로 계산
mae_val = mean_absolute_error(y,pred)
print('RMSLE: {0:.3f}, RMSE: {1:.3F}, MAE: {2:.3F}'.format(rmsle_val, rmse_val, mae_val))
로그 변환, 피처 인코딩과 모델/학습/예측/평가
from sklearn.model_selection import train_test_split , GridSearchCV
from sklearn.linear_model import LinearRegression , Ridge , Lasso
y_target = bike_df['count']
X_features = bike_df.drop(['count'],axis=1,inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size=0.3, random_state=0)
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
pred = lr_reg.predict(X_test)
evaluate_regr(y_test ,pred)def get_top_error_data(y_test, pred, n_tops = 5):
# DataFrame에 컬럼들로 실제 대여횟수(count)와 예측 값을 서로 비교 할 수 있도록 생성.
result_df = pd.DataFrame(y_test.values, columns=['real_count'])
result_df['predicted_count']= np.round(pred)
result_df['diff'] = np.abs(result_df['real_count'] - result_df['predicted_count'])
# 예측값과 실제값이 가장 큰 데이터 순으로 출력.
print(result_df.sort_values('diff', ascending=False)[:n_tops])
get_top_error_data(y_test,pred,n_tops=5)y_target.hist()y_log_transform = np.log1p(y_target)
y_log_transform.hist()# 타겟 컬럼인 count 값을 log1p 로 Log 변환
y_target_log = np.log1p(y_target)
# 로그 변환된 y_target_log를 반영하여 학습/테스트 데이터 셋 분할
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target_log, test_size=0.3, random_state=0)
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
pred = lr_reg.predict(X_test)
# 테스트 데이터 셋의 Target 값은 Log 변환되었으므로 다시 expm1를 이용하여 원래 scale로 변환
y_test_exp = np.expm1(y_test)
# 예측 값 역시 Log 변환된 타겟 기반으로 학습되어 예측되었으므로 다시 exmpl으로 scale변환
pred_exp = np.expm1(pred)
evaluate_regr(y_test_exp ,pred_exp)coef = pd.Series(lr_reg.coef_, index=X_features.columns)
coef_sort = coef.sort_values(ascending=False)
sns.barplot(x=coef_sort.values, y=coef_sort.index)# 'year', month', 'day', hour'등의 피처들을 One Hot Encoding
X_features_ohe = pd.get_dummies(X_features, columns=['year', 'month','day', 'hour', 'holiday',
'workingday','season','weather'])# 원-핫 인코딩이 적용된 feature 데이터 세트 기반으로 학습/예측 데이터 분할.
X_train, X_test, y_train, y_test = train_test_split(X_features_ohe, y_target_log,
test_size=0.3, random_state=0)
# 모델과 학습/테스트 데이터 셋을 입력하면 성능 평가 수치를 반환
def get_model_predict(model, X_train, X_test, y_train, y_test, is_expm1=False):
model.fit(X_train, y_train)
pred = model.predict(X_test)
if is_expm1 :
y_test = np.expm1(y_test)
pred = np.expm1(pred)
print('###',model.__class__.__name__,'###')
evaluate_regr(y_test, pred)
# end of function get_model_predict
# model 별로 평가 수행
lr_reg = LinearRegression()
ridge_reg = Ridge(alpha=10)
lasso_reg = Lasso(alpha=0.01)
for model in [lr_reg, ridge_reg, lasso_reg]:
get_model_predict(model,X_train, X_test, y_train, y_test,is_expm1=True)coef = pd.Series(lr_reg.coef_ , index=X_features_ohe.columns)
coef_sort = coef.sort_values(ascending=False)[:20]
sns.barplot(x=coef_sort.values , y=coef_sort.index)from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
# 랜덤 포레스트, GBM, XGBoost, LightGBM model 별로 평가 수행
rf_reg = RandomForestRegressor(n_estimators=500)
gbm_reg = GradientBoostingRegressor(n_estimators=500)
xgb_reg = XGBRegressor(n_estimators=500)
lgbm_reg = LGBMRegressor(n_estimators=500)
for model in [rf_reg, gbm_reg, xgb_reg, lgbm_reg]:
# XGBoost의 경우 DataFrame이 입력 될 경우 버전에 따라 오류 발생 가능. ndarray로 변환.
get_model_predict(model,X_train.values, X_test.values, y_train.values, y_test.values,is_expm1=True)10 회귀 실습 - 케글 주택 가격: 고급 회귀 기법
데이터 사전처리
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
house_df_org = pd.read_csv('house_price.csv')
house_df = house_df_org.copy()
house_df.head(3)print('데이터 세트의 Shape:', house_df.shape)
print('\n전체 feature 들의 type \n',house_df.dtypes.value_counts())
isnull_series = house_df.isnull().sum()
print('\nNull 컬럼과 그 건수:\n ', isnull_series[isnull_series > 0].sort_values(ascending=False))plt.title('Original Sale Price Histogram')
sns.distplot(house_df['SalePrice'])plt.title('Log Transformed Sale Price Histogram')
log_SalePrice = np.log1p(house_df['SalePrice'])
sns.distplot(log_SalePrice)# SalePrice 로그 변환
original_SalePrice = house_df['SalePrice']
house_df['SalePrice'] = np.log1p(house_df['SalePrice'])
# Null 이 너무 많은 컬럼들과 불필요한 컬럼 삭제
house_df.drop(['Id','PoolQC' , 'MiscFeature', 'Alley', 'Fence','FireplaceQu'], axis=1 , inplace=True)
# Drop 하지 않는 숫자형 Null컬럼들은 평균값으로 대체
house_df.fillna(house_df.mean(),inplace=True)
# Null 값이 있는 피처명과 타입을 추출
null_column_count = house_df.isnull().sum()[house_df.isnull().sum() > 0]
print('## Null 피처의 Type :\n', house_df.dtypes[null_column_count.index])print('get_dummies() 수행 전 데이터 Shape:', house_df.shape)
house_df_ohe = pd.get_dummies(house_df)
print('get_dummies() 수행 후 데이터 Shape:', house_df_ohe.shape)
null_column_count = house_df_ohe.isnull().sum()[house_df_ohe.isnull().sum() > 0]
print('## Null 피처의 Type :\n', house_df_ohe.dtypes[null_column_count.index])
선형 회귀 모델 학습/예측/평가
def get_rmse(model):
pred = model.predict(X_test)
mse = mean_squared_error(y_test , pred)
rmse = np.sqrt(mse)
print('{0} 로그 변환된 RMSE: {1}'.format(model.__class__.__name__,np.round(rmse, 3)))
return rmse
def get_rmses(models):
rmses = [ ]
for model in models:
rmse = get_rmse(model)
rmses.append(rmse)
return rmsesfrom sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
y_target = house_df_ohe['SalePrice']
X_features = house_df_ohe.drop('SalePrice',axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size=0.2, random_state=156)
# LinearRegression, Ridge, Lasso 학습, 예측, 평가
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge()
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso()
lasso_reg.fit(X_train, y_train)
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)def get_top_bottom_coef(model):
# coef_ 속성을 기반으로 Series 객체를 생성. index는 컬럼명.
coef = pd.Series(model.coef_, index=X_features.columns)
# + 상위 10개 , - 하위 10개 coefficient 추출하여 반환.
coef_high = coef.sort_values(ascending=False).head(10)
coef_low = coef.sort_values(ascending=False).tail(10)
return coef_high, coef_lowdef visualize_coefficient(models):
# 3개 회귀 모델의 시각화를 위해 3개의 컬럼을 가지는 subplot 생성
fig, axs = plt.subplots(figsize=(24,10),nrows=1, ncols=3)
fig.tight_layout()
# 입력인자로 받은 list객체인 models에서 차례로 model을 추출하여 회귀 계수 시각화.
for i_num, model in enumerate(models):
# 상위 10개, 하위 10개 회귀 계수를 구하고, 이를 판다스 concat으로 결합.
coef_high, coef_low = get_top_bottom_coef(model)
coef_concat = pd.concat( [coef_high , coef_low] )
# 순차적으로 ax subplot에 barchar로 표현. 한 화면에 표현하기 위해 tick label 위치와 font 크기 조정.
axs[i_num].set_title(model.__class__.__name__+' Coeffiecents', size=25)
axs[i_num].tick_params(axis="y",direction="in", pad=-120)
for label in (axs[i_num].get_xticklabels() + axs[i_num].get_yticklabels()):
label.set_fontsize(22)
sns.barplot(x=coef_concat.values, y=coef_concat.index , ax=axs[i_num])
# 앞 예제에서 학습한 lr_reg, ridge_reg, lasso_reg 모델의 회귀 계수 시각화.
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)from sklearn.model_selection import cross_val_score
def get_avg_rmse_cv(models):
for model in models:
# 분할하지 않고 전체 데이터로 cross_val_score( ) 수행. 모델별 CV RMSE값과 평균 RMSE 출력
rmse_list = np.sqrt(-cross_val_score(model, X_features, y_target,
scoring="neg_mean_squared_error", cv = 5))
rmse_avg = np.mean(rmse_list)
print('\n{0} CV RMSE 값 리스트: {1}'.format( model.__class__.__name__, np.round(rmse_list, 3)))
print('{0} CV 평균 RMSE 값: {1}'.format( model.__class__.__name__, np.round(rmse_avg, 3)))
# 앞 예제에서 학습한 lr_reg, ridge_reg, lasso_reg 모델의 CV RMSE값 출력
models = [lr_reg, ridge_reg, lasso_reg]
get_avg_rmse_cv(models)from sklearn.model_selection import GridSearchCV
def print_best_params(model, params):
grid_model = GridSearchCV(model, param_grid=params,
scoring='neg_mean_squared_error', cv=5)
grid_model.fit(X_features, y_target)
rmse = np.sqrt(-1* grid_model.best_score_)
print('{0} 5 CV 시 최적 평균 RMSE 값: {1}, 최적 alpha:{2}'.format(model.__class__.__name__,
np.round(rmse, 4), grid_model.best_params_))
return grid_model.best_estimator_
ridge_params = { 'alpha':[0.05, 0.1, 1, 5, 8, 10, 12, 15, 20] }
lasso_params = { 'alpha':[0.001, 0.005, 0.008, 0.05, 0.03, 0.1, 0.5, 1,5, 10] }
best_rige = print_best_params(ridge_reg, ridge_params)
best_lasso = print_best_params(lasso_reg, lasso_params)# 앞의 최적화 alpha값으로 학습데이터로 학습, 테스트 데이터로 예측 및 평가 수행.
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge(alpha=12)
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso(alpha=0.001)
lasso_reg.fit(X_train, y_train)
# 모든 모델의 RMSE 출력
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)
# 모든 모델의 회귀 계수 시각화
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)from scipy.stats import skew
# object가 아닌 숫자형 피쳐의 컬럼 index 객체 추출.
features_index = house_df.dtypes[house_df.dtypes != 'object'].index
# house_df에 컬럼 index를 [ ]로 입력하면 해당하는 컬럼 데이터 셋 반환. apply lambda로 skew( )호출
skew_features = house_df[features_index].apply(lambda x : skew(x))
# skew 정도가 1 이상인 컬럼들만 추출.
skew_features_top = skew_features[skew_features > 1]
print(skew_features_top.sort_values(ascending=False))house_df[skew_features_top.index] = np.log1p(house_df[skew_features_top.index])# Skew가 높은 피처들을 로그 변환 했으므로 다시 원-핫 인코딩 적용 및 피처/타겟 데이터 셋 생성,
house_df_ohe = pd.get_dummies(house_df)
y_target = house_df_ohe['SalePrice']
X_features = house_df_ohe.drop('SalePrice',axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size=0.2, random_state=156)
# 피처들을 로그 변환 후 다시 최적 하이퍼 파라미터와 RMSE 출력
ridge_params = { 'alpha':[0.05, 0.1, 1, 5, 8, 10, 12, 15, 20] }
lasso_params = { 'alpha':[0.001, 0.005, 0.008, 0.05, 0.03, 0.1, 0.5, 1,5, 10] }
best_ridge = print_best_params(ridge_reg, ridge_params)
best_lasso = print_best_params(lasso_reg, lasso_params)# 앞의 최적화 alpha값으로 학습데이터로 학습, 테스트 데이터로 예측 및 평가 수행.
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge(alpha=10)
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso(alpha=0.001)
lasso_reg.fit(X_train, y_train)
# 모든 모델의 RMSE 출력
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)
# 모든 모델의 회귀 계수 시각화
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)plt.scatter(x = house_df_org['GrLivArea'], y = house_df_org['SalePrice'])
plt.ylabel('SalePrice', fontsize=15)
plt.xlabel('GrLivArea', fontsize=15)
plt.show()# GrLivArea와 SalePrice 모두 로그 변환되었으므로 이를 반영한 조건 생성.
cond1 = house_df_ohe['GrLivArea'] > np.log1p(4000)
cond2 = house_df_ohe['SalePrice'] < np.log1p(500000)
outlier_index = house_df_ohe[cond1 & cond2].index
print('아웃라이어 레코드 index :', outlier_index.values)
print('아웃라이어 삭제 전 house_df_ohe shape:', house_df_ohe.shape)
# DataFrame의 index를 이용하여 아웃라이어 레코드 삭제.
house_df_ohe.drop(outlier_index , axis=0, inplace=True)
print('아웃라이어 삭제 후 house_df_ohe shape:', house_df_ohe.shape)y_target = house_df_ohe['SalePrice']
X_features = house_df_ohe.drop('SalePrice',axis=1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size=0.2, random_state=156)
ridge_params = { 'alpha':[0.05, 0.1, 1, 5, 8, 10, 12, 15, 20] }
lasso_params = { 'alpha':[0.001, 0.005, 0.008, 0.05, 0.03, 0.1, 0.5, 1,5, 10] }
best_ridge = print_best_params(ridge_reg, ridge_params)
best_lasso = print_best_params(lasso_reg, lasso_params)# 앞의 최적화 alpha값으로 학습데이터로 학습, 테스트 데이터로 예측 및 평가 수행.
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
ridge_reg = Ridge(alpha=8)
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso(alpha=0.001)
lasso_reg.fit(X_train, y_train)
# 모든 모델의 RMSE 출력
models = [lr_reg, ridge_reg, lasso_reg]
get_rmses(models)
# 모든 모델의 회귀 계수 시각화
models = [lr_reg, ridge_reg, lasso_reg]
visualize_coefficient(models)
회귀 트리 모델 학습/예측/평가
from xgboost import XGBRegressor
xgb_params = {'n_estimators':[1000]}
xgb_reg = XGBRegressor(n_estimators=1000, learning_rate=0.05,
colsample_bytree=0.5, subsample=0.8)
best_xgb = print_best_params(xgb_reg, xgb_params)from lightgbm import LGBMRegressor
lgbm_params = {'n_estimators':[1000]}
lgbm_reg = LGBMRegressor(n_estimators=1000, learning_rate=0.05, num_leaves=4,
subsample=0.6, colsample_bytree=0.4, reg_lambda=10, n_jobs=-1)
best_lgbm = print_best_params(lgbm_reg, lgbm_params)# 모델의 중요도 상위 20개의 피처명과 그때의 중요도값을 Series로 반환.
def get_top_features(model):
ftr_importances_values = model.feature_importances_
ftr_importances = pd.Series(ftr_importances_values, index=X_features.columns )
ftr_top20 = ftr_importances.sort_values(ascending=False)[:20]
return ftr_top20
def visualize_ftr_importances(models):
# 2개 회귀 모델의 시각화를 위해 2개의 컬럼을 가지는 subplot 생성
fig, axs = plt.subplots(figsize=(24,10),nrows=1, ncols=2)
fig.tight_layout()
# 입력인자로 받은 list객체인 models에서 차례로 model을 추출하여 피처 중요도 시각화.
for i_num, model in enumerate(models):
# 중요도 상위 20개의 피처명과 그때의 중요도값 추출
ftr_top20 = get_top_features(model)
axs[i_num].set_title(model.__class__.__name__+' Feature Importances', size=25)
#font 크기 조정.
for label in (axs[i_num].get_xticklabels() + axs[i_num].get_yticklabels()):
label.set_fontsize(22)
sns.barplot(x=ftr_top20.values, y=ftr_top20.index , ax=axs[i_num])
# 앞 예제에서 print_best_params( )가 반환한 GridSearchCV로 최적화된 모델의 피처 중요도 시각화
models = [best_xgb, best_lgbm]
visualize_ftr_importances(models)
회귀 모델들의 예측 결과 혼합을 통한 최종 예측
def get_rmse_pred(preds):
for key in preds.keys():
pred_value = preds[key]
mse = mean_squared_error(y_test , pred_value)
rmse = np.sqrt(mse)
print('{0} 모델의 RMSE: {1}'.format(key, rmse))
# 개별 모델의 학습
ridge_reg = Ridge(alpha=8)
ridge_reg.fit(X_train, y_train)
lasso_reg = Lasso(alpha=0.001)
lasso_reg.fit(X_train, y_train)
# 개별 모델 예측
ridge_pred = ridge_reg.predict(X_test)
lasso_pred = lasso_reg.predict(X_test)
# 개별 모델 예측값 혼합으로 최종 예측값 도출
pred = 0.4 * ridge_pred + 0.6 * lasso_pred
preds = {'최종 혼합': pred,
'Ridge': ridge_pred,
'Lasso': lasso_pred}
#최종 혼합 모델, 개별모델의 RMSE 값 출력
get_rmse_pred(preds)xgb_reg = XGBRegressor(n_estimators=1000, learning_rate=0.05,
colsample_bytree=0.5, subsample=0.8)
lgbm_reg = LGBMRegressor(n_estimators=1000, learning_rate=0.05, num_leaves=4,
subsample=0.6, colsample_bytree=0.4, reg_lambda=10, n_jobs=-1)
xgb_reg.fit(X_train, y_train)
lgbm_reg.fit(X_train, y_train)
xgb_pred = xgb_reg.predict(X_test)
lgbm_pred = lgbm_reg.predict(X_test)
pred = 0.5 * xgb_pred + 0.5 * lgbm_pred
preds = {'최종 혼합': pred,
'XGBM': xgb_pred,
'LGBM': lgbm_pred}
get_rmse_pred(preds)
스태킹 앙상블 모델을 통한 회귀 예측
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
# 개별 기반 모델에서 최종 메타 모델이 사용할 학습 및 테스트용 데이터를 생성하기 위한 함수.
def get_stacking_base_datasets(model, X_train_n, y_train_n, X_test_n, n_folds ):
# 지정된 n_folds값으로 KFold 생성.
kf = KFold(n_splits=n_folds, shuffle=False, random_state=0)
#추후에 메타 모델이 사용할 학습 데이터 반환을 위한 넘파이 배열 초기화
train_fold_pred = np.zeros((X_train_n.shape[0] ,1 ))
test_pred = np.zeros((X_test_n.shape[0],n_folds))
print(model.__class__.__name__ , ' model 시작 ')
for folder_counter , (train_index, valid_index) in enumerate(kf.split(X_train_n)):
#입력된 학습 데이터에서 기반 모델이 학습/예측할 폴드 데이터 셋 추출
print('\t 폴드 세트: ',folder_counter,' 시작 ')
X_tr = X_train_n[train_index]
y_tr = y_train_n[train_index]
X_te = X_train_n[valid_index]
#폴드 세트 내부에서 다시 만들어진 학습 데이터로 기반 모델의 학습 수행.
model.fit(X_tr , y_tr)
#폴드 세트 내부에서 다시 만들어진 검증 데이터로 기반 모델 예측 후 데이터 저장.
train_fold_pred[valid_index, :] = model.predict(X_te).reshape(-1,1)
#입력된 원본 테스트 데이터를 폴드 세트내 학습된 기반 모델에서 예측 후 데이터 저장.
test_pred[:, folder_counter] = model.predict(X_test_n)
# 폴드 세트 내에서 원본 테스트 데이터를 예측한 데이터를 평균하여 테스트 데이터로 생성
test_pred_mean = np.mean(test_pred, axis=1).reshape(-1,1)
#train_fold_pred는 최종 메타 모델이 사용하는 학습 데이터, test_pred_mean은 테스트 데이터
return train_fold_pred , test_pred_mean# get_stacking_base_datasets( )은 넘파이 ndarray를 인자로 사용하므로 DataFrame을 넘파이로 변환.
X_train_n = X_train.values
X_test_n = X_test.values
y_train_n = y_train.values
# 각 개별 기반(Base)모델이 생성한 학습용/테스트용 데이터 반환.
ridge_train, ridge_test = get_stacking_base_datasets(ridge_reg, X_train_n, y_train_n, X_test_n, 5)
lasso_train, lasso_test = get_stacking_base_datasets(lasso_reg, X_train_n, y_train_n, X_test_n, 5)
xgb_train, xgb_test = get_stacking_base_datasets(xgb_reg, X_train_n, y_train_n, X_test_n, 5)
lgbm_train, lgbm_test = get_stacking_base_datasets(lgbm_reg, X_train_n, y_train_n, X_test_n, 5)# 개별 모델이 반환한 학습 및 테스트용 데이터 세트를 Stacking 형태로 결합.
Stack_final_X_train = np.concatenate((ridge_train, lasso_train,
xgb_train, lgbm_train), axis=1)
Stack_final_X_test = np.concatenate((ridge_test, lasso_test,
xgb_test, lgbm_test), axis=1)
# 최종 메타 모델은 라쏘 모델을 적용.
meta_model_lasso = Lasso(alpha=0.0005)
#기반 모델의 예측값을 기반으로 새롭게 만들어진 학습 및 테스트용 데이터로 예측하고 RMSE 측정.
meta_model_lasso.fit(Stack_final_X_train, y_train)
final = meta_model_lasso.predict(Stack_final_X_test)
mse = mean_squared_error(y_test , final)
rmse = np.sqrt(mse)
print('스태킹 회귀 모델의 최종 RMSE 값은:', rmse)'머신러닝' 카테고리의 다른 글
| [ECC 스터디] 7장 군집화 (0) | 2024.11.29 |
|---|---|
| [ECC 머신러닝 스터디] 6장 차원 축소 (0) | 2024.11.22 |
| [ECC 파이썬 머신러닝 완벽가이드] 4.7-4.11 (1) | 2024.11.09 |
| [파이썬 머신러닝 완벽 가이드] 3장 평가 (1) | 2024.10.10 |
| 1장 파이썬 기반의 머신러닝 생태계의 이해 (0) | 2024.09.27 |